다면체 골격 전자쌍 이론

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

다면체 골격 전자쌍 이론은 클러스터 화합물의 구조를 예측하는 데 사용되는 이론으로, 4n, 5n, 6n 규칙을 포함한다. 4n 규칙은 보레인 및 카보레인과 같은 클러스터의 구조를 예측하며, 델타헤드론을 기반으로 한다. 5n 규칙은 3-연결 다면체를 기반으로 하며, 6n 규칙은 고리를 기반으로 하는 구조를 예측한다. 이 이론은 클러스터 내의 전자 수를 통해 구조를 예측하며, 아이소로벌 정점 단위 및 클러스터 화합물의 결합 특성도 고려한다.

더 읽어볼만한 페이지

클러스터 화학 - 철-황 클러스터
철-황 클러스터는 철과 황 원자의 결합으로 이루어진 무기화합물로서, 생체 내 단백질의 구성요소로 중요한 역할을 하며, Fe:S 화학량론에 따라 다양한 형태로 존재하고 전자전달, 촉매작용 등에 필수적이며, 여러 분야에서 응용될 수 있다.
클러스터 화학 - 철-황 단백질
철-황 단백질은 철 이온과 황 이온을 함유하며 시스테인 잔기와 결합하여 4Fe–4S, 3Fe–4S, 2Fe–2S 클러스터 형태로 존재하며, 전자 전달, 효소 보조 인자 등 생화학적 기능에 관여하고 세균과 효모의 다양한 시스템을 통해 생합성 경로가 연구된다.
유기금속화학 - 그리냐르 시약
그리냐르 시약은 할로겐화 알킬과 마그네슘을 에테르 용매에서 반응시켜 얻는 유기금속 화합물로, 강한 친핵성과 염기성을 이용하여 다양한 유기 화합물 합성에 널리 쓰이며 수분과 산소에 민감하여 무수 조건에서 취급해야 한다.
유기금속화학 - 유기 발광 다이오드
유기 발광 다이오드(OLED)는 유기 화합물의 자체 발광 현상을 이용한 소자로, 1987년 코닥의 2층 구조 소자 개발 이후 효율과 수명이 향상되어 스마트폰, TV 등 다양한 분야에 상용화되었으며, 높은 명암비와 빠른 응답 속도 등의 장점과 함께 수명 및 번인 현상 등의 단점을 극복하기 위한 기술 개발이 진행 중이다.
무기화학 - 알칼리
알칼리는 아랍어에서 유래하여 식물 재를 의미하며, 물에 녹아 수산화 이온을 생성하고 pH가 높으며 부식성이 있고 피부에 미끈거리는 특징을 보이는 물질을 지칭하며, 염기의 하위 집합으로 알칼리 금속 또는 알칼리 토금속의 염기성 염, 또는 물에 녹아 수산화 이온을 형성하는 염기를 포함한다.
무기화학 - 동소체
동소체는 동일한 원소로 이루어졌으나 원자 배열의 차이로 물리화학적 성질이 다른 물질을 지칭하며, 탄소의 다이아몬드와 흑연, 산소의 산소와 오존 등이 대표적인 예시이다.

다면체 골격 전자쌍 이론
일반 정보
이름	다면체 골격 전자쌍 이론
다른 이름	웨이드-밍고스 규칙
분야	화학
하위 분야	유기금속화학 붕소화학
관련 인물	케네스 웨이드 마이클 밍고스
개요
설명	다면체 붕소 화합물 및 관련 클러스터의 구조를 예측하는 데 사용되는 전자 계수 규칙
적용 대상	붕소 화합물 카보레인 금속 카보닐 클러스터
규칙
골격 전자쌍 수	분자 구조 예측에 사용
구조 유형	클로소 니도 아라크노 하이포
클러스터 유형별 전자쌍 계산
클로소	n + 1 전자쌍
니도	n + 2 전자쌍
아라크노	n + 3 전자쌍
하이포	n + 4 전자쌍
활용
구조 예측	다양한 클러스터 화합물의 구조를 예측하는 데 사용
결합 분석	클러스터 내의 결합 특성 이해
역사적 배경
웨이드의 기여	1971년, 다면체 붕소 화합물의 구조와 전자 수의 관계 제시
밍고스의 기여	웨이드의 연구를 확장하여 금속 카보닐 클러스터에 적용
추가 정보
참고 문헌	웨이드, K. (1971). J. Chem. Soc. D, 1971, 792–793.
관련 항목	분자 궤도 함수 이론 결합 이론

2. 클러스터 화합물의 구조 예측

다면체 골격 전자쌍 이론(PSEPT)은 클러스터 화합물의 구조를 예측하는 데 사용되며, 각 정점(꼭짓점)당 평균 전자 수에 따라 다른 규칙이 적용된다.

4''n'' 규칙: 정점당 약 4개의 전자를 갖는 클러스터(보레인, 카보레인 등)에 주로 적용된다. 이 규칙을 따르는 클러스터는 모든 면이 삼각형인 델타헤드론 또는 여기서 일부 정점이 제거된 구조(예: ''nido-'', ''arachno-'')를 가진다.
5''n'' 규칙: 정점당 전자 수가 5개에 가까워지면 적용된다. 이 클러스터들은 각 정점이 다른 세 정점과 연결된 3-연결 다면체를 기반으로 하는 구조를 형성하는 경향이 있다.
6''n'' 규칙: 전자 수가 더 증가하여 정점당 평균 6개에 가까워지면 적용될 수 있다. 이러한 클러스터는 주로 고리 형태의 구조를 가진다.

분자 궤도 함수 이론은 이러한 4''n'', 5''n'', 6''n'' 규칙을 따르는 다양한 클러스터 화합물의 화학 결합을 설명하고 합리화하는 데 사용될 수 있다.

2. 1. 4''n'' 규칙

나비형 클러스터 화합물 [Re₄(CO)₁₂]²⁻의 구조는 다면체 골격 전자쌍 이론(PSEPT)의 예측을 따른다.

각 정점당 전자 수에 따라 다른 규칙(4''n'', 5''n'', 또는 6''n'')이 적용된다.

4''n'' 규칙은 많은 보레인과 카보레인의 경우와 같이, 정점당 약 4개의 전자를 갖는 클러스터의 구조를 예측하는 데 비교적 정확하다. 이러한 클러스터의 경우, 구조는 모든 면이 삼각형인 델타헤드론을 기반으로 한다. 4''n'' 클러스터는 완전한 (''closo-'') 델타헤드론, 또는 델타헤드론에서 1개 (''nido-''), 2개 (''arachno-''), 또는 3개 (''hypho-'')의 정점이 누락되었는지 여부에 따라 ''closo-'', ''nido-'', ''arachno-'', 또는 ''hypho-''로 분류된다.

그러나 ''hypho'' 클러스터는 전자 수가 높아서 반결합 궤도를 채우기 시작하고 4''n'' 구조를 불안정하게 만들기 때문에 비교적 드물다. 전자 수가 정점당 5개의 전자에 가까우면 구조는 종종 3-연결 다면체를 기반으로 하는 5''n'' 규칙에 의해 지배되는 구조로 변경된다.

전자 수가 더 증가함에 따라 5''n'' 전자 수를 가진 클러스터의 구조는 불안정해지므로 6''n'' 규칙을 구현할 수 있다. 6''n'' 클러스터는 링을 기반으로 하는 구조를 갖는다.

분자 궤도 함수 처리는 4''n'', 5''n'', 및 6''n'' 유형의 클러스터 화합물의 결합을 합리화하는 데 사용될 수 있다.

2. 1. 1. 4''n'' 규칙의 델타헤드론

다음의 다면체는 ''closo'' 다면체이며, 4''n'' 규칙의 기초가 된다. 각 다면체는 삼각 면을 가지고 있다.^[10] 클러스터의 꼭짓점 수는 구조가 기반으로 하는 다면체를 결정한다.

꼭짓점 수	다면체
4	사면체
5	삼각쌍뿔
6	팔면체
7	오각쌍뿔
8	비틀어 늘린 사각쌍뿔 (D_2d 삼각십이면체)
9	삼중증강 삼각기둥
10	자이로 늘린 사각쌍뿔 (이중 캡 사각 반각기둥)
11	십팔면체 (가장자리 축약 이십면체)
12	이십면체 (이중 캡 오각 반각기둥)

전자 수를 사용하여 예측된 구조를 찾을 수 있다. ''n''은 클러스터 내 꼭짓점의 수이다. 4''n'' 규칙은 다음 표에 요약되어 있다.

전자 수	이름	예측된 구조
4n − 2	이중 캡 closo	n − 2 꼭짓점 closo 다면체에 2개의 캡(증강된) 면
4n	캡 closo	1개의 면이 캡된 n − 1 꼭짓점 closo 다면체
4n + 2	closo	n개의 꼭짓점을 가진 closo 다면체
4n + 4	nido	1개의 꼭짓점이 없는 n + 1 꼭짓점 closo 다면체
4n + 6	arachno	2개의 꼭짓점이 없는 n + 2 꼭짓점 closo 다면체
4n + 8	hypho	3개의 꼭짓점이 없는 n + 3 꼭짓점 closo 다면체
4n + 10	klado	4개의 꼭짓점이 없는 n + 4 꼭짓점 closo 다면체

각 클러스터에 대한 전자를 계산할 때는 원자가 전자 수를 센다. 각 전이 금속이 존재할 경우, 총 전자 수에서 10개의 전자를 뺀다. 예를 들어, Rh₆(CO)₁₆에서 총 전자 수는 6 × 9 + 16 × 2 − 6 × 10 = 86 – 60 = 26이다. 따라서, 이 클러스터는 ''n'' = 6이고, 4''n'' + 2 = 26이므로 ''closo'' 다면체이다.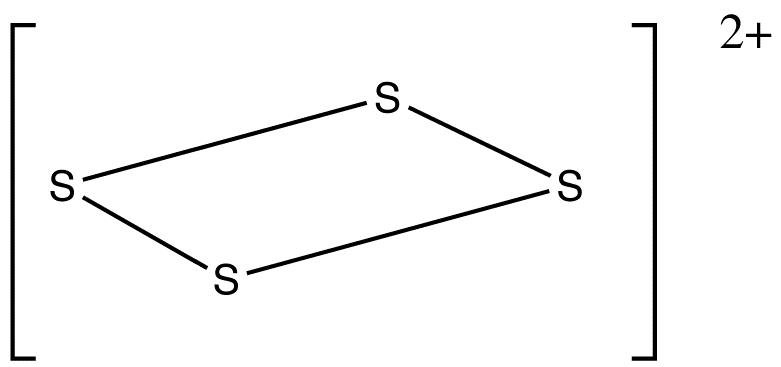

클러스터의 구조를 예측할 때 다른 규칙도 고려할 수 있다.

# 대부분 전이 금속으로 구성된 클러스터의 경우, 존재하는 모든 주족 원소는 꼭짓점보다는 배위자 또는 간극 원자로 계산하는 것이 좋다.

# 크고 전기양성적인 원자는 연결성이 높은 꼭짓점을 차지하는 경향이 있고, 작고 전기음성적인 원자는 연결성이 낮은 꼭짓점을 차지하는 경향이 있다.

# 보란 클러스터의 특별한 경우, 3개 이상의 꼭짓점에 연결된 각 붕소 원자는 1개의 말단 수소화물을 가지고 있으며, 다른 두 개의 꼭짓점에 연결된 붕소 원자는 2개의 말단 수소 원자를 갖는다. 더 많은 수소 원자가 존재하는 경우, 꼭짓점의 배위수를 균등하게 하기 위해 열린 면 위치에 배치된다.

# 전이 금속 클러스터의 특별한 경우, 배위자는 금속 중심에 추가되어 금속에 적절한 배위수를 부여하고, 수소 원자가 존재할 경우 꼭짓점의 배위수를 균등하게 하기 위해 가교 위치에 배치된다.

일반적으로, ''n''개의 꼭짓점을 가진 ''closo'' 구조는 ''n''-꼭짓점 다면체이다.

''nido'' 클러스터의 구조를 예측하려면, ''n'' + 1개의 꼭짓점을 가진 ''closo'' 클러스터를 시작점으로 사용한다. 클러스터가 작은 원자로 구성된 경우, 연결성이 높은 꼭짓점을 제거하고, 클러스터가 큰 원자로 구성된 경우, 연결성이 낮은 꼭짓점을 제거한다.

''arachno'' 클러스터의 구조를 예측하려면, ''n'' + 2개의 꼭짓점을 가진 ''closo'' 다면체를 시작점으로 사용하고, 위의 규칙에 따라 ''n'' + 1 꼭짓점 ''nido'' 복합체를 생성한다. 클러스터가 대부분 작은 원자로 구성된 경우, 첫 번째 꼭짓점에 인접한 두 번째 꼭짓점을 제거하고, 클러스터가 대부분 큰 원자로 구성된 경우, 첫 번째 꼭짓점에 인접하지 않은 두 번째 꼭짓점을 제거한다.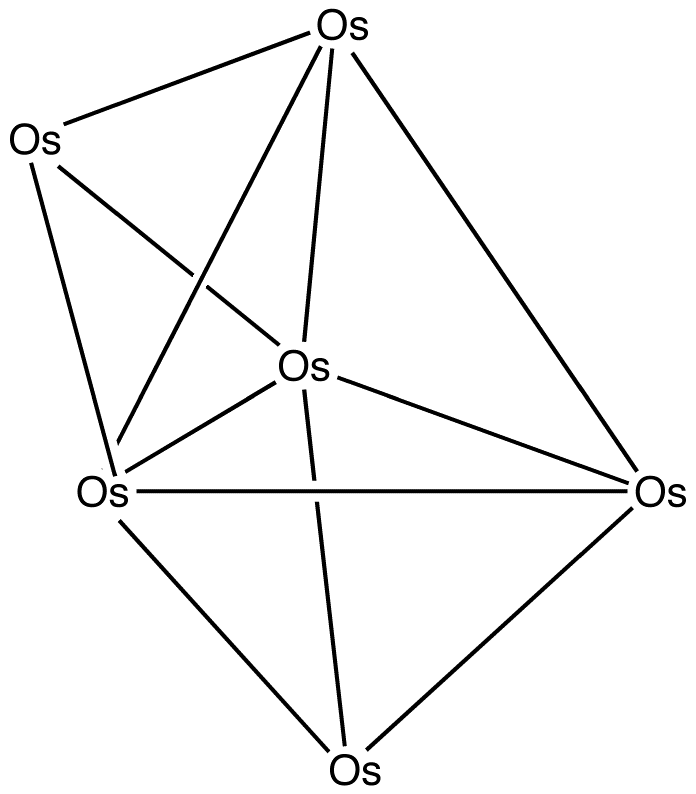

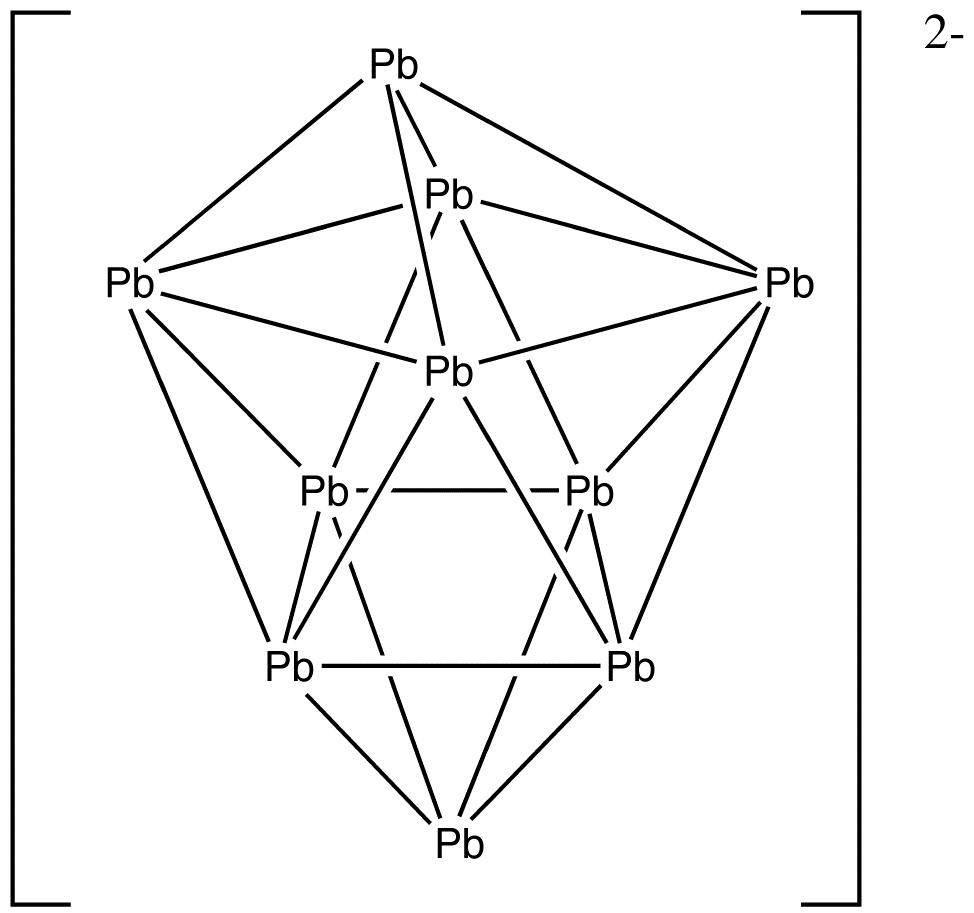
예시: Pb₁₀²⁻

: 전자 수: 10 × Pb + 2 (음전하) = 10 × 4 + 2 = 42개 전자.

: ''n'' = 10이므로, 4''n'' + 2 = 42이고, 따라서 이 클러스터는 ''closo'' 이중 캡 사각 반각기둥이다.
예시: S₄²⁺

: 전자 수: 4 × S – 2 (양전하) = 4 × 6 – 2 = 22개 전자.

: ''n'' = 4이므로, 4''n'' + 6 = 22이고, 따라서 이 클러스터는 ''arachno''이다.

: 팔면체에서 시작하여, 연결성이 높은 꼭짓점을 제거한 다음, 인접하지 않은 꼭짓점을 제거한다.
예시: Os₆(CO)₁₈

: 전자 수: 6 × Os + 18 × CO – 60 (6개의 오스뮴 원자) = 6 × 8 + 18 × 2 – 60 = 24

: ''n'' = 6이므로, 4''n'' = 24이고, 따라서 이 클러스터는 캡 ''closo''이다.

: 삼각쌍뿔에서 시작하여, 면을 캡한다. 명확성을 위해 카르보닐이 생략되었다.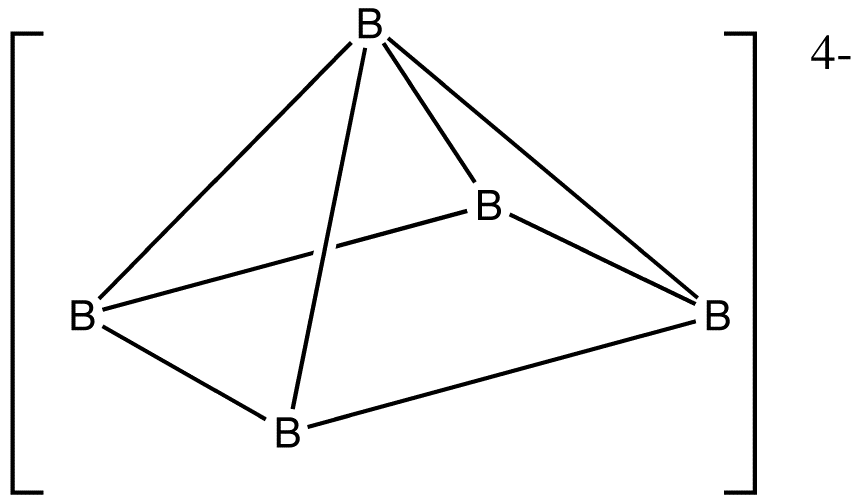

예시:^[11] B₅H₅⁴⁻

: 전자 수: 5 × B + 5 × H + 4 (음전하) = 5 × 3 + 5 × 1 + 4 = 24

: ''n'' = 5이므로, 4''n'' + 4 = 24이고, 따라서 이 클러스터는 nido이다.

: 팔면체에서 시작하여, 꼭짓점 중 하나를 제거한다.

이 규칙은 또한 카보란의 구조를 예측하는 데에도 유용하다.
예시: C₂B₇H₁₃

: 전자 수 = 2 × C + 7 × B + 13 × H = 2 × 4 + 7 × 3 + 13 × 1 = 42

: 이 경우 n = 9이므로, 4''n'' + 6 = 42이고, 클러스터는 ''arachno''이다.

델타면체 클러스터의 기록 관리는 총 전자 수 대신 골격 전자를 계산하여 수행되기도 한다. 델타면체 클러스터의 네 가지 유형에 대한 골격 궤도(전자 쌍) 및 골격 전자 수는 다음과 같다.

''n''-꼭짓점 ''closo'': ''n'' + 1 골격 궤도, 2''n'' + 2 골격 전자
''n''-꼭짓점 ''nido'': ''n'' + 2 골격 궤도, 2''n'' + 4 골격 전자
''n''-꼭짓점 ''arachno'': ''n'' + 3 골격 궤도, 2''n'' + 6 골격 전자
''n''-꼭짓점 ''hypho'': ''n'' + 4 골격 궤도, 2''n'' + 8 골격 전자

골격 전자 수는 다음 전자 수의 합계를 더하여 결정된다.

각 BH 단위에서 2개
각 CH 단위에서 3개
각 추가 수소 원자에서 1개 (BH 및 CH 단위에 있는 수소 원자 이상)
음이온 전하 전자

2. 1. 2. 4''n'' 규칙의 구조 예측

다음의 다면체는 ''closo'' 다면체이며, 4''n'' 규칙의 기초가 된다. 각 다면체는 삼각 면을 가지고 있다.^[10] 클러스터의 꼭짓점 수는 구조가 기반으로 하는 다면체를 결정한다.

꼭짓점 수	다면체
4	사면체
5	삼각 쌍뿔
6	팔면체
7	오각 쌍뿔
8	D_2d (삼각) 십이면체 (스너브 사다리꼴)
9	삼중 증강 삼각 기둥
10	자이로 연장 사각 쌍뿔
11	가장자리 축약 이십면체 (십팔면체)
12	이십면체

전자 수를 사용하여 예측된 구조를 찾을 수 있다. ''n''은 클러스터 내 꼭짓점의 수이다. 4''n'' 규칙은 다음 표에 요약되어 있다.

전자 수	이름	예측된 구조
4n − 2	이중 캡 closo	n − 2 꼭짓점 closo 다면체에 2개의 캡(증강된) 면
4n	캡 closo	1개의 면이 캡된 n − 1 꼭짓점 closo 다면체
4n + 2	closo	n개의 꼭짓점을 가진 closo 다면체
4n + 4	nido	1개의 꼭짓점이 없는 n + 1 꼭짓점 closo 다면체
4n + 6	arachno	2개의 꼭짓점이 없는 n + 2 꼭짓점 closo 다면체
4n + 8	hypho	3개의 꼭짓점이 없는 n + 3 꼭짓점 closo 다면체
4n + 10	klado	4개의 꼭짓점이 없는 n + 4 꼭짓점 closo 다면체

각 클러스터에 대한 전자를 계산할 때는 원자가 전자 수를 센다. 각 전이 금속이 존재할 경우, 총 전자 수에서 10개의 전자를 뺀다. 예를 들어, Rh₆(CO)₁₆에서 총 전자 수는 6 × 9 + 16 × 2 − 6 × 10 = 86 – 60 = 26이다. 따라서, 이 클러스터는 ''n'' = 6이고, 4''n'' + 2 = 26이므로 ''closo'' 다면체이다.

클러스터의 구조를 예측할 때 다른 규칙도 고려할 수 있다.

대부분 전이 금속으로 구성된 클러스터의 경우, 존재하는 모든 주족 원소는 꼭짓점보다는 배위자 또는 간극 원자로 계산하는 것이 좋다.
크고 전기양성적인 원자는 연결성이 높은 꼭짓점을 차지하는 경향이 있고, 작고 전기음성적인 원자는 연결성이 낮은 꼭짓점을 차지하는 경향이 있다.
보란 클러스터의 특별한 경우, 3개 이상의 꼭짓점에 연결된 각 붕소 원자는 1개의 말단 수소화물을 가지고 있으며, 다른 두 개의 꼭짓점에 연결된 붕소 원자는 2개의 말단 수소 원자를 갖는다. 더 많은 수소 원자가 존재하는 경우, 꼭짓점의 배위수를 균등하게 하기 위해 열린 면 위치에 배치된다.
전이 금속 클러스터의 특별한 경우, 배위자는 금속 중심에 추가되어 금속에 적절한 배위수를 부여하고, 수소 원자가 존재할 경우 꼭짓점의 배위수를 균등하게 하기 위해 가교 위치에 배치된다.

일반적으로, ''n''개의 꼭짓점을 가진 ''closo'' 구조는 ''n''-꼭짓점 다면체이다.

''nido'' 클러스터의 구조를 예측하려면, ''n'' + 1개의 꼭짓점을 가진 ''closo'' 클러스터를 시작점으로 사용한다. 클러스터가 작은 원자로 구성된 경우, 연결성이 높은 꼭짓점을 제거하고, 클러스터가 큰 원자로 구성된 경우, 연결성이 낮은 꼭짓점을 제거한다.

''arachno'' 클러스터의 구조를 예측하려면, ''n'' + 2개의 꼭짓점을 가진 ''closo'' 다면체를 시작점으로 사용하고, 위의 규칙에 따라 ''n'' + 1 꼭짓점 ''nido'' 복합체를 생성한다. 클러스터가 대부분 작은 원자로 구성된 경우, 첫 번째 꼭짓점에 인접한 두 번째 꼭짓점을 제거하고, 클러스터가 대부분 큰 원자로 구성된 경우, 첫 번째 꼭짓점에 인접하지 않은 두 번째 꼭짓점을 제거한다.

'''예시: Pb₁₀²⁻'''

:전자 수: 10 × Pb + 2 (음전하) = 10 × 4 + 2 = 42개 전자.

:''n'' = 10이므로, 4''n'' + 2 = 42이고, 따라서 이 클러스터는 ''closo'' 이중 캡 사각 반각기둥이다.

'''예시: S₄²⁺'''

:전자 수: 4 × S – 2 (양전하) = 4 × 6 – 2 = 22개 전자.

:''n'' = 4이므로, 4''n'' + 6 = 22이고, 따라서 이 클러스터는 ''arachno''이다.

:팔면체에서 시작하여, 연결성이 높은 꼭짓점을 제거한 다음, 인접하지 않은 꼭짓점을 제거한다.

'''예시: Os₆(CO)₁₈'''

:전자 수: 6 × Os + 18 × CO – 60 (6개의 오스뮴 원자) = 6 × 8 + 18 × 2 – 60 = 24

:''n'' = 6이므로, 4''n'' = 24이고, 따라서 이 클러스터는 캡 ''closo''이다.

:삼각 쌍뿔에서 시작하여, 면을 캡한다. 명확성을 위해 카르보닐이 생략되었다.

'''예시:^[11] B₅H₅⁴⁻'''

:전자 수: 5 × B + 5 × H + 4 (음전하) = 5 × 3 + 5 × 1 + 4 = 24

:''n'' = 5이므로, 4''n'' + 4 = 24이고, 따라서 이 클러스터는 nido이다.

:팔면체에서 시작하여, 꼭짓점 중 하나를 제거한다.

이 규칙은 또한 카보란의 구조를 예측하는 데에도 유용하다.

'''예시: C₂B₇H₁₃'''

:전자 수 = 2 × C + 7 × B + 13 × H = 2 × 4 + 7 × 3 + 13 × 1 = 42

:이 경우 n = 9이므로, 4''n'' + 6 = 42이고, 클러스터는 ''arachno''이다.

델타헤드럴 클러스터에 대한 기록 관리는 총 전자 수 대신 골격 전자를 계산하여 수행되는 경우가 있다. 델타헤드럴 클러스터의 네 가지 유형에 대한 골격 궤도(전자 쌍) 및 골격 전자 수는 다음과 같다.

''n''-꼭짓점 ''closo'': ''n'' + 1 골격 궤도, 2''n'' + 2 골격 전자
''n''-꼭짓점 ''nido'': ''n'' + 2 골격 궤도, 2''n'' + 4 골격 전자
''n''-꼭짓점 ''arachno'': ''n'' + 3 골격 궤도, 2''n'' + 6 골격 전자
''n''-꼭짓점 ''hypho'': ''n'' + 4 골격 궤도, 2''n'' + 8 골격 전자

골격 전자 수는 다음 전자 수의 합계를 더하여 결정된다.

각 BH 단위에서 2개
각 CH 단위에서 3개
각 추가 수소 원자에서 1개 (BH 및 CH 단위에 있는 수소 원자 이상)
음이온 전하 전자

2. 1. 3. 구조 예측 시 추가 규칙

대부분 전이 금속으로 구성된 클러스터의 경우, 존재하는 모든 주족 원소는 꼭짓점보다는 배위자 또는 간극 원자로 간주하는 것이 좋다.
크고 전기양성적인 원자는 연결성이 높은 꼭짓점을 차지하는 경향이 있고, 작고 전기음성적인 원자는 연결성이 낮은 꼭짓점을 차지하는 경향이 있다.
보란 클러스터의 특별한 경우, 3개 이상의 꼭짓점에 연결된 각 붕소 원자는 1개의 말단 수소화물을 가지며, 다른 두 개의 꼭짓점에 연결된 붕소 원자는 2개의 말단 수소 원자를 갖는다. 더 많은 수소 원자가 존재하는 경우, 꼭짓점의 배위수를 균등하게 하기 위해 열린 면 위치에 배치된다.
전이 금속 클러스터의 특별한 경우, 배위자는 금속 중심에 추가되어 금속에 적절한 배위수를 부여하고, 수소 원자가 존재할 경우 꼭짓점의 배위수를 균등하게 하기 위해 가교 위치에 배치된다.

2. 1. 4. ''nido'' 및 ''arachno'' 클러스터 구조 예측

''nido'' 클러스터의 구조를 예측하려면, ''n'' + 1개의 꼭짓점을 가진 ''closo'' 클러스터를 시작점으로 사용한다. 클러스터가 작은 원자로 구성된 경우, 연결성이 높은 꼭짓점을 제거하고, 클러스터가 큰 원자로 구성된 경우, 연결성이 낮은 꼭짓점을 제거한다.^[10] 이는 일반적으로 크고 전기양성적인 원자는 연결성이 높은 꼭짓점을 차지하고, 작고 전기음성적인 원자는 연결성이 낮은 꼭짓점을 차지하는 경향이 있기 때문이다.

''arachno'' 클러스터의 구조를 예측하려면, ''n'' + 2개의 꼭짓점을 가진 ''closo'' 다면체를 시작점으로 사용하고, 위의 규칙에 따라 ''n'' + 1 꼭짓점 ''nido'' 복합체를 생성한다. 클러스터가 대부분 작은 원자로 구성된 경우, 첫 번째로 제거된 꼭짓점에 인접한 두 번째 꼭짓점을 제거하고, 클러스터가 대부분 큰 원자로 구성된 경우, 첫 번째로 제거된 꼭짓점에 인접하지 않은 두 번째 꼭짓점을 제거한다.^[10]

'''예시: B₅H₅⁴⁻'''^[11]

전자 수: 5 × B + 5 × H + 4 (음전하) = 5 × 3 + 5 × 1 + 4 = 24개 전자.
''n'' = 5이므로, 4''n'' + 4 = 24이고, 따라서 이 클러스터는 ''nido''이다.
팔면체에서 시작하여, 꼭짓점 중 하나를 제거하여 구조를 예측한다.

'''예시: S₄²⁺'''

전자 수: 4 × S – 2 (양전하) = 4 × 6 – 2 = 22개 전자.
''n'' = 4이므로, 4''n'' + 6 = 22이고, 따라서 이 클러스터는 ''arachno''이다.
팔면체에서 시작하여, 연결성이 높은 꼭짓점을 제거한 다음(황은 상대적으로 전기음성적이므로 연결성이 낮은 꼭짓점을 선호), 인접하지 않은 꼭짓점을 제거하여 구조를 예측한다.

'''예시: C₂B₇H₁₃'''

전자 수 = 2 × C + 7 × B + 13 × H = 2 × 4 + 7 × 3 + 13 × 1 = 42개 전자.
이 경우 ''n'' = 9 (탄소와 붕소 원자의 수)이므로, 4''n'' + 6 = 4 × 9 + 6 = 42이고, 클러스터는 ''arachno''이다. 이는 11-꼭짓점 ''closo'' 다면체(가장자리 축약 이십면체)에서 두 개의 꼭짓점을 제거하여 구조를 예측할 수 있음을 의미한다.

2. 1. 5. 예시

Pb₁₀²⁻:전자 수: 10 × Pb + 2 (음전하) = 10 × 4 + 2 = 42개 전자.

:''n'' = 10이므로, 4''n'' + 2 = 42이고, 따라서 이 클러스터는 ''closo'' 이중 캡 사각 반각기둥 구조이다.
S₄²⁺:전자 수: 4 × S – 2 (양전하) = 4 × 6 – 2 = 22개 전자.

:''n'' = 4이므로, 4''n'' + 6 = 22이고, 따라서 이 클러스터는 ''arachno'' 구조이다.

:팔면체 구조에서 시작하여, 연결성이 높은 꼭짓점을 제거한 다음, 제거된 꼭짓점과 인접하지 않은 다른 꼭짓점을 제거하여 구조를 예측한다.
Os₆(CO)₁₈:전자 수: 6 × Os + 18 × CO – 60 (6개의 오스뮴 원자는 전이 금속이므로 각각 10개의 전자를 뺌) = 6 × 8 + 18 × 2 – 60 = 24개 전자.

:''n'' = 6이므로, 4''n'' = 24이고, 따라서 이 클러스터는 캡 ''closo'' 구조이다.

:삼각 쌍뿔 구조에서 시작하여, 하나의 면을 캡(cap)하여 구조를 예측한다. 명확성을 위해 그림에서는 카보닐기(CO)가 생략되었다.
B₅H₅⁴⁻^[11]

:전자 수: 5 × B + 5 × H + 4 (음전하) = 5 × 3 + 5 × 1 + 4 = 24개 전자.

:''n'' = 5이므로, 4''n'' + 4 = 24이고, 따라서 이 클러스터는 ''nido'' 구조이다.

:팔면체 구조에서 시작하여, 꼭짓점 중 하나를 제거하여 구조를 예측한다.

이 규칙은 카보란의 구조를 예측하는 데에도 유용하다.
C₂B₇H₁₃:전자 수 = 2 × C + 7 × B + 13 × H = 2 × 4 + 7 × 3 + 13 × 1 = 42개 전자.

:이 경우 ''n'' = 9이므로, 4''n'' + 6 = 42이고, 클러스터는 ''arachno'' 구조이다.

2. 1. 6. 골격 전자 계산

델타헤드럴 클러스터의 전자 수를 기록하고 관리하는 방법으로, 총 전자 수를 세는 대신 골격 전자만을 계산하는 방식이 사용되기도 한다. 델타헤드럴 클러스터의 네 가지 주요 유형에 따른 골격 궤도(전자쌍)와 골격 전자 수는 다음과 같다.

클러스터 유형 (n = 꼭짓점 수)	골격 궤도 수	골격 전자 수
n-꼭짓점 closo	n + 1	2n + 2
n-꼭짓점 nido	n + 2	2n + 4
n-꼭짓점 arachno	n + 3	2n + 6
n-꼭짓점 hypho	n + 4	2n + 8

골격 전자 수는 다음 규칙에 따라 각 구성 요소가 기여하는 전자의 수를 합하여 결정된다.

각 붕소-수소(BH) 단위: 2개
각 탄소-수소(CH) 단위: 3개
기본 단위(BH, CH)에 포함된 수소 원자 외에 추가로 존재하는 각 수소 원자: 1개
음이온 전하: 음전하의 수만큼 더함

2. 2. 5''n'' 규칙

꼭짓점당 전자 수가 5개에 가까워지는 클러스터의 경우, 구조는 4''n'' 규칙 대신 5''n'' 규칙을 따르는 경향이 있다. 5''n'' 규칙은 각 꼭짓점이 다른 세 꼭짓점과 연결된 3-연결 다면체를 기반으로 구조를 예측한다. 이 3-연결 다면체는 모든 면이 삼각형인 델타다면체의 쌍대 다면체에 해당한다.

2. 2. 1. 5''n'' 규칙의 3-연결 다면체

앞서 논의된 4''n'' 규칙은 주로 4''n'' + ''k''개의 전자 수를 가진 클러스터를 다루며, 각 꼭짓점에는 약 4개의 전자가 있다. 꼭짓점당 전자가 더 많이 추가되면, 꼭짓점당 전자 수는 5에 가까워진다. 델타다면체를 기반으로 하는 구조 대신, 5''n''형 클러스터는 각 꼭짓점이 다른 3개의 꼭짓점과 연결된 3-연결 다면체라는 다른 종류의 다면체를 기반으로 하는 구조를 가진다. 3-연결 다면체는 델타 다면체의 쌍대 다면체이다. 일반적인 유형의 3-연결 다면체는 아래 표와 같다.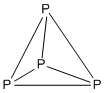

꼭짓점 수	3-연결 다면체의 유형
4	사면체
6	삼각기둥
8	정육면체
10	오각기둥
12	D_2d 유사 팔면체 (스너브 사다리꼴의 쌍대)
14	삼각 증폭 삼각기둥의 쌍대 (K₅ 결합체)
16	정사각형 절단 사다리꼴
18	가장자리 수축된 이십면체의 쌍대
20	십이면체

5''n'' 규칙은 총 전자 수에 따라 클러스터의 구조를 예측하며, 그 내용은 다음과 같다.

총 전자 수	예상 구조
5n	n-꼭짓점 3-연결 다면체
5n + 1	n – 1 꼭짓점 3-연결 다면체에 한 꼭짓점이 모서리에 삽입됨
5n + 2	n – 2 꼭짓점 3-연결 다면체에 두 꼭짓점이 모서리에 삽입됨
5n + k	n − k 꼭짓점 3-연결 다면체에 k개의 꼭짓점이 모서리에 삽입됨

'''예시'''

'''P₄'''
: 전자 수 계산: 4 × P = 4 × 5 = 20
: 이 클러스터는 총 20개의 전자를 가지며, 이는 ''n'' = 4일 때 5''n'' 규칙(5 × 4 = 20)을 만족한다. 따라서 P₄는 4개의 꼭짓점을 가진 3-연결 다면체인 사면체 구조를 가진다.

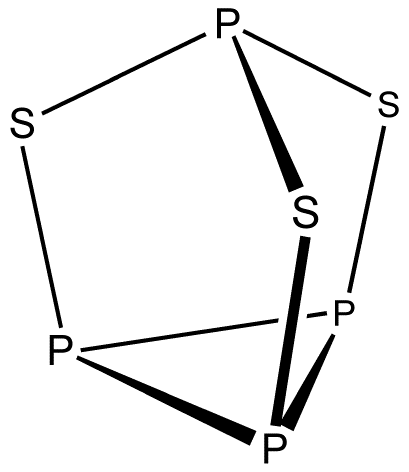
'''P₄S₃'''
: 전자 수 계산: 4 × P + 3 × S = 4 × 5 + 3 × 6 = 38
: 이 클러스터는 총 38개의 전자를 가지며, 이는 ''n'' = 7일 때 5''n'' + 3 규칙(5 × 7 + 3 = 38)을 만족한다. 따라서 P₄S₃는 ''n'' - ''k'' = 7 - 3 = 4개의 꼭짓점을 가진 3-연결 다면체(사면체) 구조를 기본으로 하고, 여기에 3개의 꼭짓점(S 원자)이 모서리에 삽입된 형태의 구조를 가진다.

'''P₄O₆'''
: 전자 수 계산: 4 × P + 6 × O = 4 × 5 + 6 × 6 = 56
: 이 클러스터는 총 56개의 전자를 가지며, 이는 ''n'' = 10일 때 5''n'' + 6 규칙(5 × 10 + 6 = 56)을 만족한다. 따라서 P₄O₆는 ''n'' - ''k'' = 10 - 6 = 4개의 꼭짓점을 가진 3-연결 다면체(사면체) 구조를 기본으로 하고, 여기에 6개의 꼭짓점(O 원자)이 모서리에 삽입된 형태의 구조를 가진다.

2. 2. 2. 5''n'' 규칙의 구조 예측

앞서 논의한 4''n'' 규칙은 주로 4''n'' + ''k''개의 전자를 가진 클러스터를 다루며, 각 꼭짓점에는 약 4개의 전자가 있다. 꼭짓점당 전자가 더 많이 추가되면, 꼭짓점당 전자 수는 5에 가까워진다. 이 경우, 클러스터는 델타다면체 기반 구조 대신, 각 꼭짓점이 다른 세 꼭짓점과 연결된 3-연결 다면체라고 알려진 다른 종류의 다면체를 기반으로 하는 구조를 채택하는 경향이 있다. 3-연결 다면체는 델타 다면체의 쌍대다면체이다. 일반적인 3-연결 다면체의 종류는 다음과 같다.

꼭짓점 수	3-연결 다면체의 유형
4	사면체
6	삼각기둥
8	정육면체
10	오각기둥
12	D_2d 유사 팔면체 (스너브 사다리꼴의 쌍대)
14	삼각 증폭 삼각기둥의 쌍대 (K₅ 결합체)
16	정사각형 절단 사다리꼴
18	가장자리 수축된 이십면체의 쌍대
20	십이면체

5''n'' 규칙은 다음과 같이 요약될 수 있다.

총 전자 수	예상 구조
5n	n-꼭짓점 3-연결 다면체
5n + 1	n – 1 꼭짓점 3-연결 다면체에 한 꼭짓점이 모서리에 삽입됨
5n + 2	n – 2 꼭짓점 3-연결 다면체에 두 꼭짓점이 모서리에 삽입됨
5n + k	n − k 꼭짓점 3-연결 다면체에 k개의 꼭짓점이 모서리에 삽입됨

=== 예시 ===

'''P₄'''
: 전자 수: 4 × P = 4 × 5 = 20
: ''n'' = 4인 5''n'' 구조(20 = 5 × 4)이므로 사면체 구조를 가진다.

'''P₄S₃'''
: 전자 수: 4 × P + 3 × S = 4 × 5 + 3 × 6 = 38
: ''n'' = 7인 5''n'' + 3 구조(38 = 5 × 7 + 3)이다. 따라서 7 - 3 = 4개의 꼭짓점을 가진 3-연결 다면체(사면체) 구조를 기반으로 하며, 세 개의 꼭짓점(황 원자)이 모서리에 삽입된 형태이다.

'''P₄O₆''' (삼산화 사인)
: 전자 수: 4 × P + 6 × O = 4 × 5 + 6 × 6 = 56
: ''n'' = 10인 5''n'' + 6 구조(56 = 5 × 10 + 6)이다. 따라서 10 - 6 = 4개의 꼭짓점을 가진 3-연결 다면체(사면체) 구조를 기반으로 하며, 여섯 개의 꼭짓점(산소 원자)이 모서리에 삽입된 형태이다. 이는 아다만탄과 유사한 구조를 가진다.

2. 2. 3. 예시

'''P₄'''

::전자 수: 4 × P = 4 × 5 = 20

::이는 ''n'' = 4인 5''n'' 구조에 해당하므로, 사면체 구조를 가질 것으로 예상된다.

'''P₄S₃'''

::전자 수: 4 × P + 3 × S = 4 × 5 + 3 × 6 = 38

::이는 ''n'' = 7인 5''n'' + 3 구조에 해당한다. 5''n'' + ''k'' 규칙에 따라, 이는 ''n'' − ''k'' = 7 - 3 = 4개의 꼭짓점을 가진 3-연결 다면체(사면체)를 기반으로 하며, ''k'' = 3개의 꼭짓점이 모서리에 삽입된 구조로 예상된다.

'''P₄O₆'''

::전자 수: 4 × P + 6 × O = 4 × 5 + 6 × 6 = 56

::이는 ''n'' = 10인 5''n'' + 6 구조에 해당한다. 5''n'' + ''k'' 규칙에 따라, 이는 ''n'' − ''k'' = 10 - 6 = 4개의 꼭짓점을 가진 3-연결 다면체(사면체)를 기반으로 하며, ''k'' = 6개의 꼭짓점이 모서리에 삽입된 구조로 예상된다.

2. 3. 6''n'' 규칙

클러스터의 전자 수가 증가하여 꼭짓점당 평균 6개에 가까워지면, 기존의 4''n'' 또는 5''n'' 규칙 기반 구조는 불안정해진다. 이러한 전자 수가 많은 클러스터는 6''n'' 규칙을 따르는 경향이 있으며, 주로 고리를 기반으로 하는 구조를 가진다. 분자 궤도 함수 이론은 4''n'', 5''n'', 6''n'' 규칙을 따르는 클러스터 화합물의 결합을 설명하는 데 사용될 수 있다.

2. 3. 1. 6''n'' 규칙의 구조 예측

5''n'' 규칙을 따르는 클러스터에 전자가 더 추가되어 꼭짓점당 전자 수가 6에 가까워지면, 해당 클러스터는 4''n''이나 5''n'' 규칙 대신 6''n'' 규칙에 따라 고리(ring)를 기반으로 하는 구조를 형성하는 경향이 있다. 6''n'' 구조에 대한 규칙은 다음과 같다.

총 전자 수	예측된 구조
6n – k	k/2 개의 횡단 결합을 가진 n원 고리
6n – 4	2개의 횡단 결합을 가진 n원 고리
6n – 2	1개의 횡단 결합을 가진 n원 고리
6n	n원 고리
6n + 2	n원 사슬 (1개의 끊어진 결합을 가진 n원 고리)

'''S₈'''
* 전자 수 = 8 × S = 8 × 6 = 48 전자.
* ''n'' = 8이므로, 6''n'' = 48이다. 따라서 이 클러스터는 8원 고리 구조를 가진다.

'''헥산(C₆H₁₄)'''
* 전자 수 = 6 × C + 14 × H = 6 × 4 + 14 × 1 = 38 전자.
* ''n'' = 6이므로, 6''n'' = 36이고 6''n'' + 2 = 38이다. 따라서 이 클러스터는 6원 사슬 구조를 가진다.

2. 3. 2. 예시

'''S₈'''

전자 수 = 8 × S = 8 × 6 = 48 전자.
''n'' = 8이므로, 6''n'' = 48이다. 따라서 이 클러스터는 8원 고리 구조를 가진다.

'''헥산(C₆H₁₄)'''

전자 수 = 6 × C + 14 × H = 6 × 4 + 14 × 1 = 38 전자.
''n'' = 6이므로, 6''n'' = 36이고 6''n'' + 2 = 38이다. 따라서 이 클러스터는 6원 사슬 구조를 가진다.

2. 4. 아이소로벌 정점 단위

다면체 골격 전자쌍 이론에 따라, 어떤 정점 단위가 BH와 아이소로벌 관계라면 BH 단위를 대체할 수 있다. 예를 들어, BH와 CH는 등전자성이 아니지만, CH⁺ 단위는 BH와 아이소로벌 관계이므로 카보레인에서 BH를 대체할 수 있다. 이러한 관계는 각 단위의 프론티어 오비탈 분석을 통해 설명된다.^[10]

아이소로벌 원리는 전이 금속 화합물에도 적용된다. 예를 들어, Fe(CO)₃ 단위는 BH와 아이소로벌 관계이며, 클러스터 골격 결합에 2개의 전자를 제공하는 것으로 간주된다. Fe(CO)₃가 2개의 전자를 제공하는 이유는 다음과 같이 설명할 수 있다.

중심 금속인 철(Fe)은 8개의 원자가 전자를 가진다.
3개의 카보닐기(CO) 리간드는 각각 2개의 전자를 제공하여 총 6개의 전자를 더한다 (총 14 전자: 8 + 3 × 2 = 14).
금속-리간드 결합에서 3쌍(전자 6개)은 Fe–CO 시그마 결합에, 다른 3쌍(전자 6개)은 Fe에서 CO로의 π 역결합에 참여하는 것으로 간주한다.
따라서 클러스터 골격 자체에 기여하는 전자는 전체 14개 전자에서 금속-리간드 결합(시그마 및 파이 역결합)에 사용된 12개 전자를 제외한 2개가 된다.

3. 클러스터 화합물의 결합

''클로소''-B₆H₆²⁻의 경우, 붕소 원자는 팔면체의 각 꼭지점에 위치하며 sp 혼성화를 한다.^[11] 하나의 sp-혼성 궤도는 구조 바깥쪽으로 향하여 수소 원자와의 화학 결합을 형성한다. 다른 sp-혼성 궤도는 구조의 중심부로 향하여 클러스터 중심에 큰 결합 분자 궤도를 형성한다. 나머지 두 개의 비혼성화 p 궤도는 구형 구조의 접선을 따라 위치하며 붕소 꼭지점 사이에 더 많은 결합 및 반결합 궤도를 생성한다.^[9]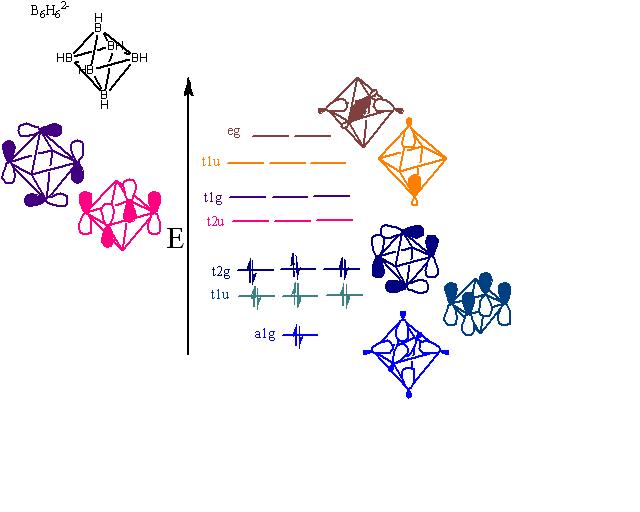

B₆H₆²⁻의 분자 궤도 그림으로, 클러스터 형성에 기여하는 궤도를 보여준다. 궤도의 그림 표현이 표시되어 있으며, T 및 E 대칭의 MO 세트는 각각 2개 또는 1개의 추가 그림 표현을 가질 수 있으며, 여기에는 표시되지 않았다.

궤도 그림은 다음과 같이 분류된다.

18개의 붕소 원자 궤도에서 파생된 18개의 골격 분자 궤도(MO)는 다음과 같다.

클러스터 중심의 1개의 결합 MO와 6개의 sp-방사형 혼성 궤도에서 파생된 5개의 반결합 MO
12개의 접선 p-궤도에서 파생된 6개의 결합 MO와 6개의 반결합 MO

따라서 총 골격 결합 궤도는 7개, 즉 ''n'' + 1개이다. (여기서 ''n''은 꼭지점의 수)

전이 금속 클러스터는 화학 결합에 d 오비탈을 사용한다. 따라서, 붕소 및 주족 원소 클러스터에 존재하는 4개 대신 최대 9개의 결합 오비탈을 갖는다.^[12]^[13] 다면체 골격 전자쌍 이론(PSEPT)은 또한 금속보레인에도 적용된다.

전이 금속은 반경이 크기 때문에 일반적으로 주족 원소보다 더 큰 클러스터를 형성한다. 크기가 커짐에 따라 이러한 클러스터는 종종 중심에 원자를 포함한다. 대표적인 예로 [Fe₆C(CO)₁₆]^2-가 있다. 이러한 경우 전자 계수 규칙은 간극 원자가 모든 원자가 전자를 클러스터 결합에 기여한다고 가정한다. 이런 식으로 [Fe₆C(CO)₁₆]^2-는 간극 탄소 원자의 기여를 고려하여 [Fe₆(CO)₁₆]^6- 또는 리간드 수를 조정한 [Fe₆(CO)₁₈]^2-와 전자적으로 유사하게 취급될 수 있다.^[14]

4. 같이 보기

스티크 규칙

참조

_[1] 논문 The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds 1971
_[2] 논문 A General Theory for Cluster and Ring Compounds of the Main Group and Transition Elements
_[3] 논문 The significance and impact of Wade's rules 2013
_[4] 논문 Structural and Bonding Patterns in Cluster Chemistry
_[5] 논문 Lecture notes distributed at the University of Illinois, Urbana-Champaign 2008
_[6] 논문 Nyholm Memorial Lectures
_[7] 논문 Polyhedral Skeletal Electron Pair Approach
_[8] 논문 A Unifying Electron-counting rule for Macropolyhedral Boranes, Metallaboranes, and Metallocenes
_[9] 논문 Electronic Requirements for Macropolyhedral Boranes
_[10] 서적 Advanced Inorganic Chemistry Wiley-Interscience
_[11] 서적 Chemical Applications of Group Theory https://archive.org/[...] John Wiley & Sons
_[12] 논문 Chemical Applications of Group Theory and Topology.7. A Graph-Theoretical Interpretation of the Bonding Topology in Polyhedral Boranes, Carboranes, and Metal Clusters
_[13] 논문 Electronic Structure of Transition Metal Cluster Complexes with Weak- and Strong-field Ligands
_[14] 서적 Encyclopedia of Inorganic Chemistry

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com